ষষ্ঠ শ্রেণি – গণিত – প্রথম অধ্যায় (স্বাভাবিক সংখ্যা ও ভগ্নাংশ) – অঙ্কপাতন, স্বকীয় মান ও স্থানীয় মানের ধারণা

অঙ্ক এবং অঙ্কপাতন

গণনার জন্য আমরা সংখ্যা ব্যবহার করি। আমরা সাধারণত দশমিক বা দশভিত্তিক সংখ্যা পদ্ধতি ব্যবহার করি, যেখানে সংখ্যাগুলো গড়ে ওঠে ১০টা প্রতীক দিয়ে- ০, ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯। এই প্রতীকগুলোকে বলা হয় অঙ্ক। তার মধ্যে শূন্য বাদে বাকি অঙ্কগুলোকে সার্থক অঙ্ক বলা হয়। শূন্যসহ এই দশটি অঙ্ক দিয়ে আমরা অসংখ্য সংখ্যা লিখতে পারি। অঙ্ক ব্যবহার করে সংখ্যা লেখাকে বলা হয় অঙ্কপাতন।

স্বকীয় মান ও স্থানীয় মানের ধারণা

রোমান সংখ্যাতে এক বোঝাতে I লেখা হয়। দশভিত্তিক পদ্ধতিতে লেখা হয় ১। কিন্তু দেখো, রোমান সংখ্যাতে দুটো এক, মানে II লিখলে অর্থ হয় ২, অথচ দশভিত্তিক পদ্ধতিতে ১১ মানে হচ্ছে ১১। এই তফাৎ কেন? চলো বোঝার চেষ্টা করি।

চলো চিন্তা করি আমরা দশভিত্তিক সংখ্যা কীভাবে লিখি। ০ থেকে ৯ পর্যন্ত তো সরাসরি অঙ্ক লেখা যায়। তারপরের সংখ্যাগুলো কীভাবে লিখবো? আমরা এখানে দুটো অঙ্ক নিই। বামদিকে ১ রাখি ডানে ০ থেকে ৯ পর্যন্ত বসিয়ে ১০ থেকে ১৯ পর্যন্ত লিখি। এরপর আবার বামদিকে ২ রেখে লিখি ২০ থেকে ২৯ পর্যন্ত, এবং এভাবে পর্যায়ক্রমে আমরা ৯৯ পর্যন্ত লিখি। তারপর ১০০-৯৯৯ পর্যন্ত আমরা তিনটি অঙ্ক দিয়ে লিখি। আরো বড় সংখ্যার জন্য চারটি, পাঁচটি বা প্রয়োজনমত যতগুলো অঙ্ক প্রয়োজন হয়।

০ থেকে ৯ পর্যন্ত প্রতিটি অঙ্কের নিজের মান হলো এর স্বকীয় মান। ১ এর স্বকীয় মান ১, ২ এর স্বকীয় মান ২ এরকম, ৫ এর স্বকীয় মান ৫ এরকম।

কিন্তু আমরা দেখছিলাম পাশাপাশি দুটো ১ লিখলে, অর্থাৎ ১১ এর মান ১+১=২ না হয়ে হয় ১১। আবার ২৪ ও ৪২ এই দুটো সংখ্যা যদি দেখি, দুটোই ২ ও ৪ ব্যবহার করে লেখা, কিন্তু তারা সমান মান প্রকাশ করছে না।

আমরা একটু চিন্তা করি যদি, ১১ এর মান আসলে (১০+১) এর সমান। একইভাবে ২৪ এর মান (২০+৪) এবং ৪২ এর মান (৪০+২) এর সমান। তাহলে দেখো, অঙ্কপাতনে সবচেয়ে ডানের যে সংখ্যা সে নিজের স্বকীয় মানের সমান মান প্রকাশ করলেও ডানদিক থেকে দ্বিতীয় সংখ্যাটি নিজের স্বকীয় মানের দশগুণ মান প্রকাশ করছে!

অর্থাৎ অঙ্কপাতনের সময় কোন অঙ্ক কোন অবস্থানে রাখা হচ্ছে, এর ওপর নির্ভর করে অঙ্কগুলোর একটা মান আছে। এই মানটা হলো স্থানীয় মান।

স্থানীয় মান কীভাবে আসছে? মনে করে দেখো, আমরা ৯ পর্যন্ত লেখার পর দশ বোঝাতে ১ এর পাশে ০ লিখেছিলাম। তাহলে যখন পরের সংখ্যা ১১ লিখছি, তখনও কিন্তু বামদিকের একের মাঝে অন্তর্নিহিতভাবে ১০ থেকে যাচ্ছে। একইভাবে ২১-এর ২-এর মধ্যে অন্তর্নিহিতভাবে ২০ আছে।

যদি এখনো কোনরকম কনফিউশন থাকে, তাহলে এই অংশটা খেয়াল করো,
৪২-এ ৪ এর স্বকীয় মান ৪, স্থানীয় মান ৪০; ২ এর স্বকীয় মান ২, স্থানীয় মান ২।
২৪-এ ৪ এর স্বকীয় মান ৪, স্থানীয় মান ৪; ২ এর স্বকীয় মান ২, স্থানীয় মান ২০।

অর্থাৎ প্রত্যেকটা অঙ্কের স্বকীয় মান সবসময় এক থাকবে। কিন্তু স্থানীয় মান সংখ্যার মধ্যে অঙ্কটা কোন জায়গাতে আছে তার ওপর নির্ভর করবে। এই হলো স্বকীয় মান আর স্থানীয় মানের ধারণা।

আরেকটু বড় উদাহরণ যদি নিই, ৫৪৭৩ = ৫০০০ + ৪০০ + ৭০ + ৩ = ৫ × ১০০০ + ৪ × ১০০ + ৭ × ১০ + ৩

এজন্য ৫৪৭৩ সংখ্যাটিতে ৫, ৪, ৭ ও ৩ অঙ্কগুলোর স্বকীয় মান যথাক্রমে ৫, ৪, ৭ ও ৩-ই হবে কিন্তু স্থানীয় মান হবে যথাক্রমে ৫০০০, ৪০০, ৭০ ও ৩। আমরা নিশ্চয়ই এখন বুঝতে পারছি স্থানীয় মান কীভাবে কাজ করে?

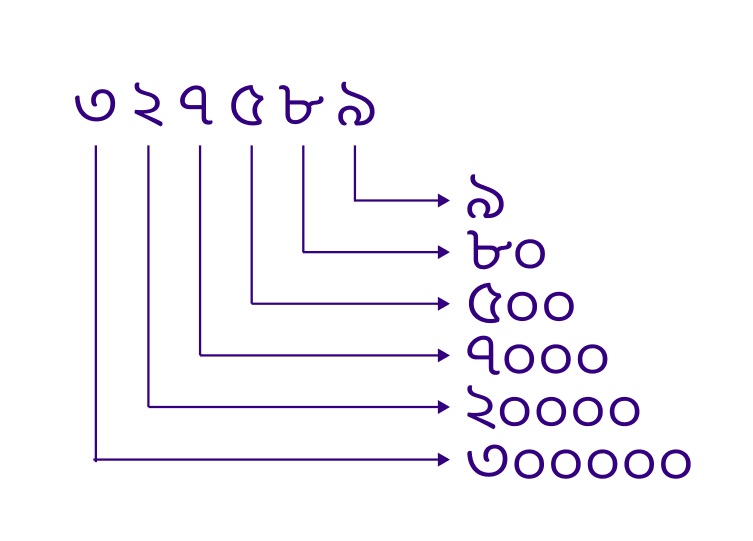
গাণিতিক সমস্যা ১: ৩২৭৫৮৯ সংখ্যাটিতে অঙ্কগুলোর স্থানীয় মান দেখাও।

সমাধান: