- প্রথম অধ্যায় (বৈজ্ঞানিক প্রক্রিয়া ও পরিমাপ) – বিজ্ঞান কীভাবে কাজ করে?
- প্রথম অধ্যায় (বৈজ্ঞানিক প্রক্রিয়া ও পরিমাপ) – রাশি, একক ও এককের বিভিন্ন পদ্ধতি
- প্রথম অধ্যায় (বৈজ্ঞানিক প্রক্রিয়া ও পরিমাপ) – দৈর্ঘ্য, প্রস্থ ও সময়ের একক
দৈর্ঘ্যের একক
দৈর্ঘ্য, প্রস্থ, উচ্চতা, গভীরতা, পুরুত্ব, দূরত্ব যে নামেই যখন ডাকি না কেন- এই সবগুলোই দৈর্ঘ্য। দৈর্ঘ্য পরিমাপের এসআই একক হলো মিটার। ১৮৭৫ সালে একটা প্লাটিনাম-ইরিডিয়াম মিশ্রিত ধাতুর দন্ডে দুটি দাগ দিয়ে 0°C তাপমাত্রায় দাগদুটোর দূরত্বকে মিটারের পরিমাণ হিসেবে নির্দিষ্ট করা হয়। ফ্রান্সের সেভেরেসে অবস্থিত ওজন ও পরিমাপের আন্তর্জাতিক সংস্থা (International Bureau of Weights and Measures)-এ এটাকে সংরক্ষণ করে রাখা হয়।
[এখানে তাপমাত্রা উল্লেখ করার কারণ হলো তাপমাত্রা বাড়ানো হলে পদার্থের প্রসারণ ঘটে, অর্থাৎ নির্দিষ্ট তাপমাত্রায় পরিমাপ না করলে সঠিক দৈর্ঘ্য পাওয়া যাবে না।]
বর্তমানে অবশ্য মিটারের সংজ্ঞা ভিন্নভাবে দেয়া হয়, আলোর বেগের হিসেবে- তবে উপস্থাপন ভিন্নভাবে করলেও পরিমাণ মূলত একই আছে। ধারণা দেয়ার জন্য- আমরা খাতায় মার্জিন করতে যে স্কেল ব্যবহার করি, তাতে সেন্টিমিটার হিসেবে ৩০ ঘর দাগ কাটা থাকে। ১ মিটারের পরিমাণ ১০০ সেন্টিমিটারের সমান, মানে তিন স্কেলের দৈর্ঘ্য থেকে একটু বেশি।
দৈর্ঘ্যের এককের গুণিতক ও ভগ্নাংশ
আমাদের অনেক সময় খুব ছোট দৈর্ঘ্য মাপি, কখনো খুব বড়। যেমন একটা পয়সার পুরুত্ব খুব ছোট্ট একটা দৈর্ঘ্য হবে, আবার এক জেলা থেকে অন্য কোন জেলার দূরত্ব মাপতে গেলে সেটা তুলনামূলক বড় একটা দৈর্ঘ্য হবে। এরকম বিভিন্ন ধরণের দৈর্ঘ্য মাপার দরকার হয়।
একটা কয়েনের পুরুত্ব ০.০০১৫ মিটার বলার থেকে ১.৫ মিলিমিটার বলাটা সুবিধাজনক। আবার ঢাকা থেকে নিউইয়র্কের দূরত্ব প্রায় ১,২৬,৫০,০০০ মিটার বলার থেকে ১২,৬৫০ কিলোমিটার বললে তা বলতে, লিখতে ও বুঝতে সুবিধাজনক।
এখানে কিলো মূলত ১০০০ গুণ এবং মিলি কথাটা ১০০০ ভাগের এক ভাগ নির্দেশ করে। যেমন ২ কিলোমিটার মানে ২×১০০০ মিটার, অর্থাৎ ২০০০ মিটার। একইভাবে ২ মিলিমিটার মানে ২ মিটারের ১০০০ ভাগের এক ভাগ, অর্থাৎ ২÷১০০০ মিটার অর্থাৎ ০.০০২ মিটার।
এরকম মেগা (১০,০০,০০০ গুণ), কিলো (১,০০০ গুণ), সেন্টি (১০০ ভাগের ১ ভাগ), মিলি (১০০০ ভাগের ১ ভাগ), মাইক্রো (১০,০০,০০০ ভাগের ১ ভাগ) প্রভৃতি গুণিতক ও ভগ্নাংশগুলো SI এককের সাথে ব্যবহার হয়ে থাকে। শুধু দৈর্ঘ্যের একক বা মিটারের ক্ষেত্রেই নয়, অন্য এককগুলোর সাথেও এগুলো ব্যবহার হয়।
আমাদের দৈনন্দিন জীবনে কিলোমিটার, মিটার, সেন্টিমিটার ও মিলিমিটার এককগুলো আমরা প্রায়ই ব্যবহার করি। নিচে এই এককগুলোর মধ্যে রূপান্তর দেখানো হলো-
১ কিলোমিটার = ১০০০ মিটার
১ মিটার = ১÷১০০০ কিলোমিটার = ০.০০১ কিলোমিটার
১ মিটার = ১০০ সেন্টিমিটার
১ সেন্টিমিটার = ১÷১০০ মিটার = ০.০১ মিটার
১ মিটার = ১০০০ মিলিমিটার
১ মিলিমিটার = ০.০০১ মিটার
১ সেন্টিমিটার = ১০ মিলিমিটার
১ মিলিমিটার = ০.১ সেন্টিমিটার
গাণিতিক সমস্যা ১: পৃথিবী থেকে চাঁদের দূরত্ব প্রায় ৩,৮৫,০০০ কিলোমিটার। একে মিটারে প্রকাশ কর।
সমাধান: ৩,৮৫,০০০ কিলোমিটার = ৩,৮৫,০০০ × ১০০০ মিটার = ৩৮,৫০,০০,০০০ মিটার
গাণিতিক সমস্যা ২: ২৫ সেন্টিমিটারকে মিটারে প্রকাশ কর।
সমাধান: ২৫ সেন্টিমিটার = ২৫ ÷ ১০০ মিটার = ০.২৫ মিটার
গাণিতিক সমস্যা ৩: ২.৫ কিলোমিটারকে মিলিমিটারে প্রকাশ কর।
সমাধান: ২.৫ কিলোমিটার = ২.৫×১০০০ মিটার = ২৫০০ মিটার = ২৫০০×১০০০ মিলিমিটার = ২৫,০০,০০০ মিলিমিটার
[মনে রাখার জন্য: কিলোমিটার মিটার থেকে বড়। সেন্টিমিটার ও মিলিমিটার মিটার থেকে ছোট। বড় থেকে ছোটতে রূপান্তরের সময় গুণ এবং ছোট থেকে বড়তে রূপান্তরের সময় ভাগ হয়।]
দৈর্ঘ্য পরিমাপ
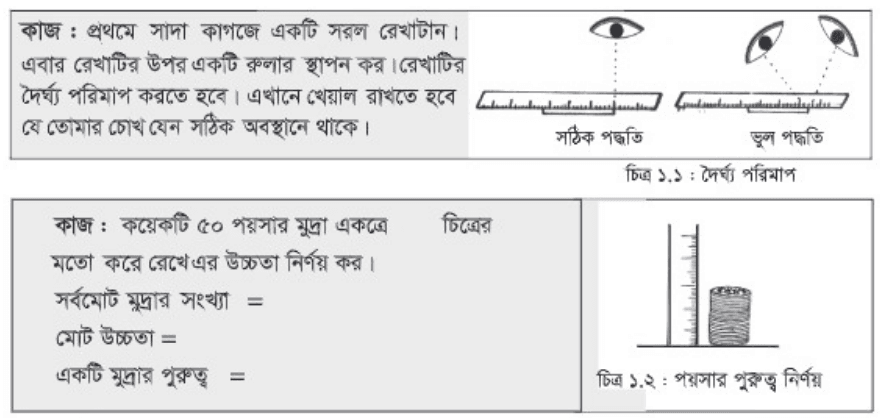
রুলার বা স্কেল দিয়ে দৈর্ঘ্য পরিমাপের ক্ষেত্রে আমাদের ওপরের ছবিতে যেভাবে দেখানো হয়েছে সেরকম দাগ বরাবর সোজাসুজি তাকানোর চেষ্টা করতে হবে। আশেপাশে থেকে তাকালে চোখের সাথে কোণ তৈরি হওয়াতে পরিমাপ কিছুটা কমবেশি হওয়ার আশঙ্কা থাকে। (একে তীর্যক ত্রুটি বলা হয়)
জ্ঞানের পাশাপাশি পরিমাপ বা পরীক্ষণের জন্য সঠিক কৌশল বের করতে পারা বেশ গুরুত্বপূর্ণ। যেমন একটা কয়েনের পুরুত্ব আমি যদি নির্ণয় করতে চাই, তা সাধারণ স্কেল দিয়ে করা বেশ কঠিন। একটা কৌশল হলো আমি যদি বেশ কয়েকটি কয়েন পরপর রেখে একসাথে পুরুত্ব মাপি। এরপর মুদ্রার সংখ্যা দিয়ে ভাগ করে নিলে একটি কয়েনের পুরুত্ব পাওয়া যাবে।
গাণিতিক সমস্যা ৬: ৫ টাকার ৮টি কয়েনের মোট পুরুত্ব ৮ মিলিমিটার। প্রতিটি কয়েনের পুরুত্ব কত?
সমাধান: প্রতিটি কয়েনের পুরুত্ব = ৮÷৫ মিলিমিটার = ১.৬ মিলিমিটার
ভরের একক
মিটারের অনুরূপভাবে প্লাটিনাম-ইরিডিয়াম ধাতুতে তৈরি একটা সিলিন্ডারের ভরকে কিলোগ্রামের আদর্শ পরিমাণ হিসেবে নির্ধারণ করা হয়েছিলো, যা ফ্রান্সের সেভেরেসে অবস্থিত ওজন ও পরিমাপের আন্তর্জাতিক সংস্থাতে (International Bureau of Weights and Measures) সংরক্ষণ করে রাখা হয়েছিলো।
বর্তমানে কোন বস্তুর পরিমাপকে আদর্শ না ধরে প্রাকৃতিক বিভিন্ন ঘটনার সাপেক্ষে এককের সংজ্ঞাগুলো দেয়ার চেষ্টা করা হয়। যেকারণে মিটারের মত ভরের সংজ্ঞাও পরিবর্তন করা হয়েছে। সংজ্ঞাটা বুঝতে পদার্থবিজ্ঞানের বেশ কিছু জ্ঞান প্রয়োজন, যেটা আমাদের আপাতত দরকার নেই। তবে মিটারের মতই সংজ্ঞা পরিবর্তন হলেও পরিমাণ মূলত পরিবর্তন হয়নি। আমরা প্রতিদিনের জীবনে কিলোগ্রামে ভর মেপে থাকি, তাই পরিমাপটা নিয়ে আমাদের সবারই ধারণা আছে।
বেশি পরিমাণ ভর মাপার ক্ষেত্রে কুইন্টাল, মেট্রিক টন এরকম এককগুলো আমরা ব্যবহার করি। ছোট ভর মাপার ক্ষেত্রে গ্রাম ব্যবহার হয়ে থাকে এবং আরো ছোট ভরের ক্ষেত্রে মিলিগ্রাম প্রভৃতি।
১ মেট্রিক টন = ১০ কুইন্টাল
১ কুইন্টাল = ১০০ কিলোগ্রাম
১ মেট্রিক টন = ১০০০ কিলোগ্রাম
১ কিলোগ্রাম = ১০০০ গ্রাম
১ গ্রাম = ১০০০ মিলিগ্রাম
গাণিতিক সমস্যা ৫: ১ কুইন্টালে কত মেট্রিক টন?
সমাধান: ১০ কুইন্টাল = ১ মেট্রিক টন
তাহলে ১ কুইন্টাল = ১÷১০ মেট্রিক টন = ০.১ মেট্রিক টন
গাণিতিক সমস্যা ৬: ২ কিলোগ্রামকে মিলিগ্রামে প্রকাশ কর।
সমাধান: ২ কিলোগ্রাম = ২×১০০০ গ্রাম = ২০০০০ গ্রাম = ২০০০০×১০০০ মিলিগ্রাম = ২,০০,০০,০০০ মিলিগ্রাম
ভর পরিমাপ
ভর পরিমাপের জন্য আমরা দাঁড়ি পাল্লা ব্যবহার করি। বর্তমানে ডিজিটাল পাল্লা পাওয়া যায়, যেগুলো সরাসরি ভরের পরিমাপ দেখিয়ে দিতে পারে। দাঁড়ি পাল্লার ক্ষেত্রে যে পাল্লায় বেশি ভর থাকবে সে পাল্লাটি বেশি ঝুঁকে থাকবে। আমরা এক পাল্লায় বস্তু রাখি, অন্য পাল্লায় ১ কিলোগ্রাম, ৫০০ গ্রাম, ১০০ গ্রাম প্রভৃতি বিভিন্ন ভরের বাটখারা রাখতে থাকি। যখন দুটি পাল্লা সাম্যাবস্থায় আসবে, তখন মোট বাটখারার ভর থেকে বস্তুর ভর বের করতে পারি।
গাণিতিক সমস্যা ৭: এক পাল্লায় কিছু আপেল রেখে অন্য পাল্লায় দুটি ১ কিলোগ্রাম ভরের বাটখারা ও একটি ৫০০ গ্রাম ভরের বাটখারা রাখা হলে দাঁড়ি পাল্লা সাম্যাবস্থায় আসে। আপেলের ভর কত?
সমাধান: ২ কিলোগ্রাম = ২×১০০০ গ্রাম = ২০০০০ গ্রাম = ২০০০০×১০০০ মিলিগ্রাম = ২,০০,০০,০০০ মিলিগ্রাম
গাণিতিক সমস্যা ৮: এক পাল্লায় ১০০ গ্রাম ভর রাখা অবস্থায় অন্য পাল্লায় ৬ টি মার্বেল রাখা হলে দাঁড়ি পাল্লা সাম্যাবস্থায় আসলো। প্রতিটি মার্বেলের ভর কত?
সমাধান:
৬ টি মার্বেলের ভর ১০০ গ্রাম
১ টি মার্বেলের ভর = ১০০ ÷ ৬ গ্রাম = ১৬.৬৭ গ্রাম
সময়ের একক
সময়ের পরিমাপের জন্য আন্তর্জাতিক একক হলো সেকেন্ড। এখানেও মিলিসেকেন্ড, কিলোসেকেন্ড প্রভৃতি ব্যবহার করা সম্ভব, তবে আমরা প্রতিদিনের ব্যবহারে এগুলো ব্যবহার করি না- বরং আমরা সেকেন্ড, মিনিট, ঘন্টা, দিন, মাস ও বছর ব্যবহার করি।
১ বছর = ৩৬৫ দিন
১ দিন = ২৪ ঘন্টা
১ ঘন্টা = ৬০ মিনিট
১ মিনিট = ৬০ সেকেন্ড
গাণিতিক সমস্যা ৯: ১ বছরে কত সেকেন্ড?
সমাধান:
১ বছর = ৩৬৫ দিন = ৩৬৫×২৪ ঘন্টা = ৮৭৬০ ঘন্টা
= ৮৭৬০×৬০ মিনিট = ৫২৫৬০০ মিনিট
= ৫২৫৬০০×৬০ সেকেন্ড = ৩,১৫,৩৬,০০০ সেকেন্ড
সময়ের ক্রমাঞ্চন/দাগাঙ্কন

তোমাদের বইয়ে সহজভাবে একটি সূর্যঘড়ি তৈরির উপায় বলা হয়েছে। তোমাদের প্রশ্ন আসছে কি ঘড়িটা কতটুকু কাজ করবে? এটুকু তো বুঝতেই পারছো যে এটা অবশ্যই শুধু দিনের বেলা কাজ করবে, যখন সূর্যের আলো থাকবে। তাছাড়া যদি মেঘলা আকাশের কারণে ঠিকভাবে রোদ না আসে, বা আশেপাশে অন্যকিছুর ছায়াতে ঢেকে যায়, তখন এতে সময় দেখা যাবে না। এখন সারা বছরব্যাপী এটা কাজ করবে কিনা?
আমরা জানি শীতকালে দিন তুলনামূলক ছোট হয়, সন্ধ্যা আগে হয়ে যায়। গ্রীষ্মকালে দিন তুলনামূলক বড় হয়। অর্থাৎ সারাবছর সূর্যের কিরণ একইভাবে হয় না। এজন্য ঘড়িটা যখন তৈরি করা হবে, তার আগে-পরের এক-দুই মাস মোটামুটিভাবে সঠিক সময় দেখাবে। তবে পরের বছর বছর আবার একই দিন ফিরে আসলে তখন এটা সময় ঠিক দেখাবে।
একটা কৌশল হতে পারে আমি যদি বিভিন্ন ঋতুতে সময় দেখার জন্য আলাদা আলাদা এরকম ঘড়ি তৈরি করে নিই। তবে সেটার প্রয়োজন নেই, কারণ এখন আমাদের প্রযুক্তিচালিত অ্যানালগ ও ডিজিটাল ঘড়ি আছে যেগুলো খুব সূক্ষ্মভাবে সময় দেখাতে পারে।


