পরিমাপে ত্রুটি ও অনিশ্চয়তা
মনে করা যাক স্কেল দিয়ে আমরা একটা টেবিলের দৈর্ঘ্য মাপতে চাচ্ছি। কত রকমের ত্রুটি হতে পারে চিন্তা কর তো! স্কেলটাতে দাগ পুরোপুরি সঠিকভাবে না থাকতে পারে, মাপ নেয়ার সময় দেখার ভুল হতে পারে, স্কেল একাধিকবার স্থাপন করতে হলে এদিক-ওদিক হতে পারে এবং অনেকরকম ত্রুটি এখানে হওয়া সম্ভব। তবে নবম-দশম শ্রেণিতে ত্রুটির বিভিন্ন ধরণগুলো আলোচিত হয়নি, চূড়ান্ত ত্রুটি আর আপেক্ষিক ত্রুটি নিয়ে আলোচনা করা হয়েছে।
চূড়ান্ত ত্রুটি ও আপেক্ষিক ত্রুটি
চূড়ান্ত ত্রুটি (Absolute Error): পরিমাপকৃত মান ও প্রকৃত মানের পার্থক্যই চূড়ান্ত ত্রুটি (বা পরম ত্রুটি)। উদাহরণ: প্রকৃতপক্ষে 1.25 m দৈর্ঘ্যের একটি টেবিলের মাপ পরিমাপ করে বিভিন্ন ত্রুটির কারণে 1.2 m পাওয়া গেলো। তাহলো চূড়ান্ত ত্রুটি (1.25 m - 1.2 m) = 0.05 m
চূড়ান্ত ত্রুটি নির্ণয়ের ক্ষেত্রে আমরা পরিমাপকৃত মান ও প্রকৃত মানের পার্থক্যের পরম মান নিই। চূড়ান্ত ত্রুটি = |পরিমাপকৃত মান - প্রকৃত মান|
এখন 1.25 m দৈর্ঘ্য মাপতে 0.05 m বা 5 cm এদিক-ওদিক হওয়া অনেকসময়ই, বিশেষ করে বৈজ্ঞানিক পরীক্ষণের সময় বেশ গুরুত্বপূর্ণ হয়ে উঠতে পারে। আবার 10 cm ব্যাসের একটা কলমের মাপ দিতে গিয়ে 5 cm ত্রুটি হলো- এটা অনেক বড় রকম একটা ত্রুটি হবে সেক্ষেত্রে। কিন্তু আবার পৃথিবী আর সূর্যের কেন্দ্রের দূরত্ব কত, এটা হিসেব করতে 100000 km কমবেশি হওয়াটাও বেশ গ্রহণযোগ্য। তো এখানে চলে আসে আপেক্ষিক ত্রুটির ধারণা।
আপেক্ষিক ত্রুটি (Relative Error): চূড়ান্ত ত্রুটি ও পরিমাপকৃত মানের অনুপাত হলো আপেক্ষিক ত্রুটি। আপেক্ষিক ত্রুটি = চূড়ান্ত ত্রুটি / পরিমাপকৃত মান = |পরিমাপকৃত মান - প্রকৃত মান| / পরিমাপকৃত মান
[উচ্চতর শ্রেণির পাঠ্যবইগুলোতে আপেক্ষিক ত্রুটিকে পরম ত্রুটি ও প্রকৃত মানের (আপেক্ষিক মানের নয়) অনুপাত হিসেবে উল্লেখ করা হয়েছে। আমাদের আলোচনা পাঠ্যবইয়ের সাথে সামঞ্জস্যপূর্ণ রেখেছি।]
অনেক সময়ই আমরা আপেক্ষিক ত্রুটিকে শতকরা হিসেবে প্রকাশ করতে প্রিফার করি।
উদাহরণ: প্রকৃতপক্ষে 1.25 m দৈর্ঘ্যের একটি টেবিলের মাপ পরিমাপ করে বিভিন্ন ত্রুটির কারণে 1.2 m পাওয়া গেলো। চূড়ান্ত ত্রুটি আমরা পেয়েছিলাম 0.05 m। তাহলে আপেক্ষিক ত্রুটি = 0.05 m / 1.2 m = 0.04167
খেয়াল কর, আপেক্ষিক ত্রুটিতে ওপরে-নিচে m একক ভাগ হয়ে যাওয়াতে ফাইনাল রেজাল্টে কোন একক থাকছে না। এরকম যেকোন ক্ষেত্রে, একই এককে থাকা সমজাতীয় রাশির অনুপাতের কোন একক থাকে না। আপেক্ষিক ত্রুটিকে আমরা শতকরা হিসেবে লিখতে প্রিফার করি। সেক্ষেত্রে, আপেক্ষিক ত্রুটি = 0.04167 × 100% = 4.167%
অনিশ্চয়তা
ধরা যাক আমাদের কাছে নিচের ছবির মত দুটো স্কেল আছে। প্রথম স্কেলে শুধু cm-এ দাগ কাটা, দ্বিতীয় স্কেলে cm-কে দশ ভাগ করা, অর্থাৎ mm পর্যন্ত দাগ কাটা।
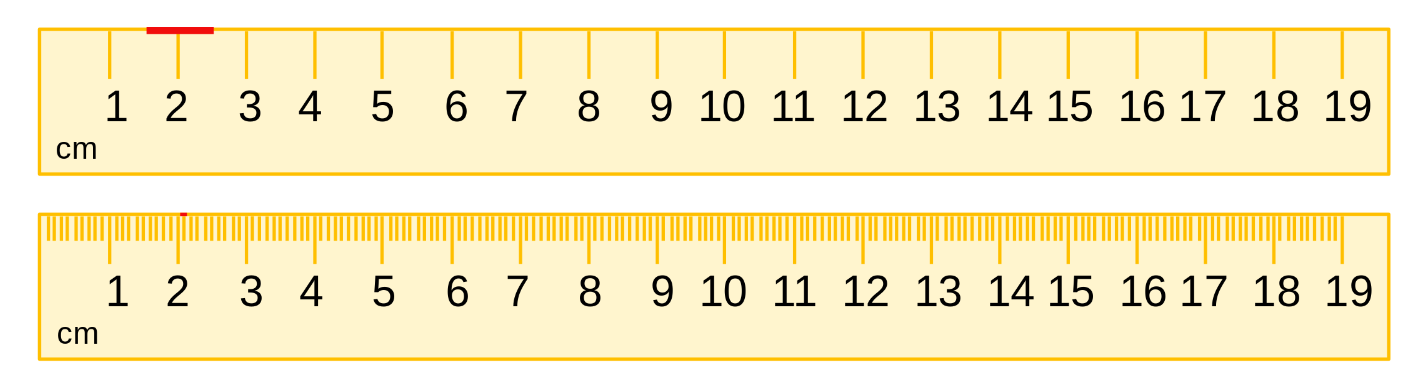 তো প্রথম স্কেলে আমরা cm-এ কোন কিছু মাপতে পারবো। কোন কিছু যে দাগের সবচেয়ে কাছাকাছি মনে হচ্ছে, সেটিকে আমরা যদি পরিমাপ ধরে নিই, তাহলে কিছুটা ত্রুটি থেকে যায়। যেমন ছবিতে লাল চিহ্নিত জায়গার মধ্যে মাপ আসলে সবচেয়ে কাছাকাছি মান হিসেবে 2 cm নেয়া যায়। যা মূলত 1.5 cm থেকে 2.5 cm পর্যন্ত হতে পারে, অর্থাৎ 2 cm মাপ পেলে বলা যায় তা 2±0.5 cm।
তো প্রথম স্কেলে আমরা cm-এ কোন কিছু মাপতে পারবো। কোন কিছু যে দাগের সবচেয়ে কাছাকাছি মনে হচ্ছে, সেটিকে আমরা যদি পরিমাপ ধরে নিই, তাহলে কিছুটা ত্রুটি থেকে যায়। যেমন ছবিতে লাল চিহ্নিত জায়গার মধ্যে মাপ আসলে সবচেয়ে কাছাকাছি মান হিসেবে 2 cm নেয়া যায়। যা মূলত 1.5 cm থেকে 2.5 cm পর্যন্ত হতে পারে, অর্থাৎ 2 cm মাপ পেলে বলা যায় তা 2±0.5 cm।
এই ±0.5 cm হলো আমাদের অনিশ্চয়তা। mm দাগ কাটা স্কেলে অনিশ্চয়তা হবে ±0.5 mm।
যে ক্ষেত্রে প্রকৃত মান জানা থাকবে না, সেখানে আমরা সম্ভাব্য সর্বোচ্চ চূড়ান্ত ত্রুটি হিসেব করি। অর্থাৎ, প্রকৃত মান না জানলে অনিশ্চয়তার মানকে আমরা চূড়ান্ত ত্রুটির পরিমাণ ধরে নিব, এবং সে অনুযায়ী হিসেব করব। আগেই বলা হয়েছে ত্রুটি নির্ণয়ের ক্ষেত্রে আমরা পরম মান নিই। অর্থাৎ ওপরের প্রথম স্কেলে কোন দৈর্ঘ্য মাপা হলে চূড়ান্ত ত্রুটি হবে |±0.5 cm| = 0.5 cm, দ্বিতীয় স্কেলের ক্ষেত্রে 0.5 mm।
গাণিতিক সমস্যা: mm দাগ কাটা একটি রুলারে একটি টেবিলের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 5 cm, 7 cm ও 8 cm পাওয়া গেলো। আয়তন পরিমাপে আপেক্ষিক ত্রুটি কত?
সমাধানের জন্য প্রথমে মনে রাখতে হবে মাপগুলো cm-এ হলেও mm দাগ কাটা স্কেলে মাপ নেয়া হয়েছে। অর্থাৎ দৈর্ঘ্য পরিমাপে চূড়ান্ত ত্রুটি 0.5 mm বা 0.05 cm। কিন্তু আমাকে আয়তন নির্ণয়ে আপেক্ষিক ত্রুটি বের করতে বলা হয়েছে, এটা আমি কীভাবে করব?
প্রথমে আমাদের পরিমাপকৃত আয়তন বের করা যাক, 5 cm x 7 cm x 8 cm = 280 cm³।
এখন দৈর্ঘ্য পরিমাপে চূড়ান্ত ত্রুটি বিবেচনায় সম্ভাব্য সর্বনিম্ন দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 4.95 cm, 6.95 cm ও 7.95 cm। তাহলে সম্ভাব্য সর্বনিম্ন আয়তন = 4.95 cm x 6.95 cm x 7.95 cm = 273.5 cm³ এভাবে হিসেব করলে চূড়ান্ত ত্রুটি = 280 cm³ - 273.5 cm³ = 6.5 cm³।
আবার, সম্ভাব্য সর্বোচ্চ দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 5.05 cm, 7.05 cm ও 8.05 cm তাহলে সম্ভাব্য সর্বোচ্চ আয়তন = 5.05 cm x 7.05 cm x 8.05 cm = 286.6 cm³ এক্ষেত্রে চূড়ান্ত ত্রুটি = 286.6 cm³ - 280 cm³ 6.6 cm³
বলেছিলাম চূড়ান্ত ত্রুটির হিসেবে আমরা সম্ভাব্য সর্বাধিকটি বিবেচনা করি। তাহলে এখানে চূড়ান্ত ত্রুটি = 6.6 cm³ হবে।
তাহলে, আপেক্ষিক ত্রুটি = 6.6 / 280 = 0.02357 = 2.357%