পরিমাপের যন্ত্রপাতি - স্কেল ও স্লাইড ক্যালিপার্স
আমরা ইতোমধ্যে আলোচনা করেছি এখনকার সময়ে পরিমাণগত গবেষণা গুরুত্বপূর্ণ হয়ে উঠেছে। তো সূক্ষ্মভাবে পরিমাপের জন্য আমাদের যন্ত্রপাতি প্রয়োজন। এমনই কিছু যন্ত্রের সাথে আমরা পরিচিত হব এখানে।
স্কেল
সাধারণত স্কুল-কলেজে আমরা যে স্কেল ব্যবহার করি তা ফুট স্কেল, যেখানে ১২ ইঞ্চি পর্যন্ত দাগ কাটা থাকে (১২ ইঞ্চিতে ১ ফুট), পাশাপাশি ৩০ সেন্টিমিটার পর্যন্ত সেন্টিমিটারেও দাগ কাটা থেকে।
মিটার স্কেল: 100 cm বা 1 m লম্বা স্কেলকে মিটার স্কেল বলে।
মিটার স্কেলে mm বা ১ মিটারের ১০০০ ভাগের ১ ভাগ পর্যন্ত মাপা যায়। যেমন: 0.364 m বা 36 cm 4 mm এখানে মাপা সম্ভব কিন্তু mm এর ভগ্নাংশ মাপা সম্ভব না।
আমরা যদি SI এককের বিষয়টি মনে রাখি, পদার্থবিজ্ঞান পড়ার সময় ইঞ্চি বা ফুট এককগুলো আমরা সাধারণত ব্যবহার করবো না। মিটার, সেন্টিমিটার, মিলিমিটার এই এককগুলোই আমরা সচারচর ব্যবহার করব।
ভার্নিয়ার ক্যালিপার্স বা স্লাইড ক্যালিপার্স
অনেক সময় আমাদের আরো সূক্ষ্ম মাপ নেয়ার প্রয়োজন পড়তে পারে। এক্ষেত্রে একটা জনপ্রিয় ইন্সট্রুমেন্ট হলো ভার্নিয়ার ক্যালিপার্স বা স্লাইড ক্যালিপার্স।
স্লাইড ক্যালিপার্স: মিটার স্কেল অপেক্ষা সূক্ষ্মতরভাবে মাপার যন্ত্র, যেখানে মিটার স্কেলের সাথে ভার্নিয়ার স্কেল ব্যবহার করা হয়। ভার্নিয়ার স্কেল: মিটার স্কেল অপেক্ষা সূক্ষ্মতরভাবে মাপার জন্য সহায়ক একটি স্কেল, যা নড়াচড়া করানো যায়।
ভার্নিয়ার স্কেলে যদি ২০টি দাগ থাকে, তবে তা প্রধান স্কেলের ক্ষুদ্রতম ১৯ দাগের সমান হয়, যদি ১০টি দাগ থাকে, তাহলে ৯ দাগের সমান হয়। অর্থাৎ প্রধান স্কেলের দাগগুলো থেকে ভার্নিয়ার স্কেলের দাগগুলো খানিকটা ছোট হয়।
ভার্নিয়ার ধ্রুবক: ভার্নিয়ার স্কেলের এক ভাগ প্রধান স্কেলের এক ভাগ থেকে যতটুকু ছোট হয় তাকে ভার্নিয়ার ধ্রুবক বলে। একে VC দ্বারা প্রকাশ করা হয়।

ভার্নিয়ার স্কেলের ছবিতে নিচে দুটো চোয়াল দেখতো পাচ্ছ, একটা চোয়াল ভার্নিয়ার স্কেলের সাথে মুভ করে। যে বস্তুটা মাপা হবে, তা চোয়ালদুটোর মধ্যে রেখে যথাযথভাবে চোয়ালগুলো যেন বস্তুর দু’পাশ স্পর্শ করে এমনভাবে সেট করে নিতে হবে।
এই অবস্থায় ভার্নিয়ার স্কেলের ০ দাগ প্রধান স্কেলের যে দাগ অতিক্রম করে, তাকে প্রধান স্কেল পাঠ বলা হয়, এটা M দিয়ে প্রকাশ করা হয়।
মনে রাখতে হবে, অবশ্যই সে দাগ নিতে হবে যে দাগ ভার্নিয়ার স্কেল অতিক্রম করবে, খুব কাছাকছি হলেও যদি অতিক্রম না করে, তবে তা নেয়া যাবে না। আসলে অতিক্রমের পর আর কতটুকু যায় সেটা পরিমাপ করাই ভার্নিয়ার স্কেলের কাজ।
ভার্নিয়ার স্কেলের কোন একটা দাগ আমরা দেখবো প্রধান স্কেলের সাথে হুবহু বা প্রায় হুবহু মিলে গেছে।
ভার্নিয়ার সমপাতন: ভার্নিয়ার স্কেলের যে দাগটি মূল স্কেলের কোন দাগের সাথে হুবহু বা প্রায় হুবহু মিলে যায়, তা হলো ভার্নিয়ার সমপাতন। একে V দিয়ে প্রকাশ করা হয়।
প্রশ্ন করতে পারো দুটো দাগ মিলে গেলে কী হবে? ধরা যাক ভার্নিয়ার স্কেলের ভাগসংখ্যা ২০, মানে ২০ ঘর প্রধান স্কেলের ১৯ ঘরের সমান। তাহলে যদি কোন দাগ মিলে যায়, ভার্নিয়ার স্কেলের ২০ দাগ পর আরেকটি দাগ মিলার কথা। যেকারণে শূন্য আর বিশতম দাগ একসাথে মিলতে পারে, অন্য কোন ক্ষেত্রে দুটো দাগ মিলে যাওয়া সম্ভব না।
স্লাইড ক্যালিপার্সে পরিমাপ
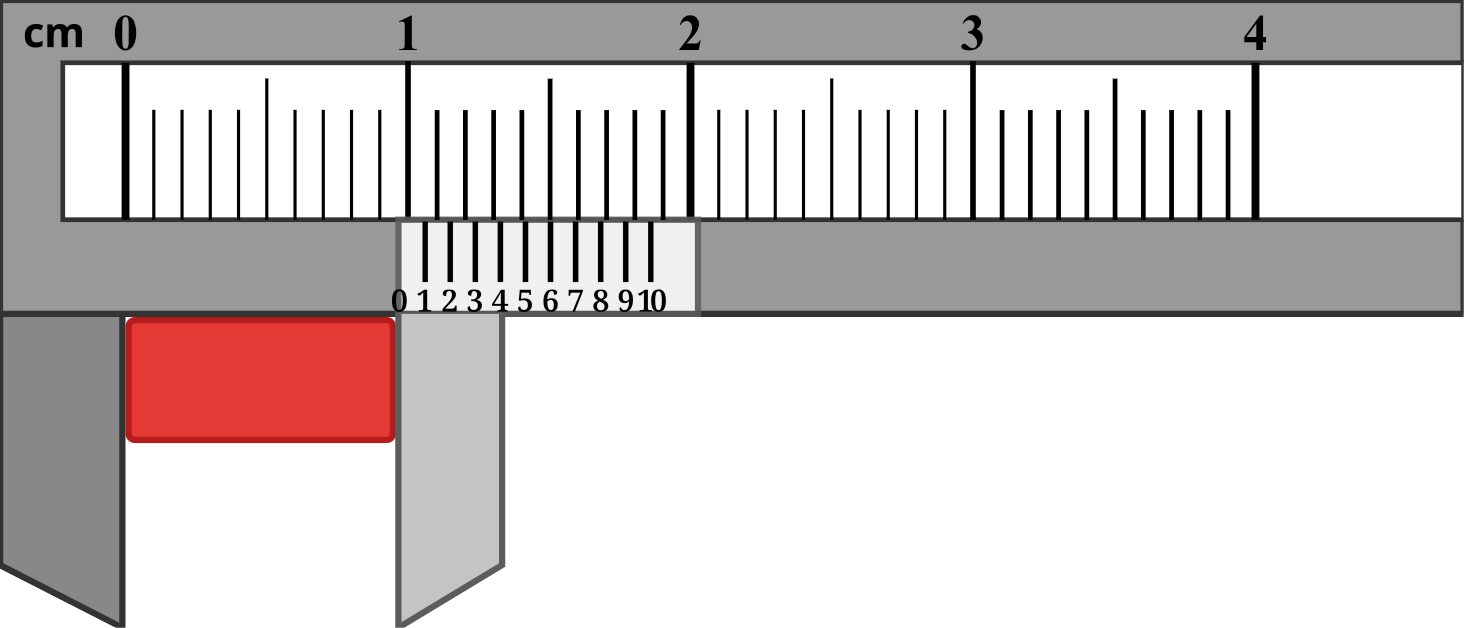
ছবির দিকে খেয়াল করি। এখানে প্রধান স্কেলে আমাদের ব্যবহার করা স্কেলের মতই 0, 1, 2 প্রভৃতি cm এককে দাগ কাটা। সেগুলো প্রতিটা আবার দশ ভাগ করা। cm-এর দশভাগের একভাগ মানে mm। তাহলে প্রধান স্কেলের ক্ষুদ্রতম একেকটা ভাগ হবে 1 mm।
প্রধান স্কেল পাঠ নির্ণয়
আমরা দেখছি ভার্নিয়ার স্কেলের শূন্য দাগ প্রধান স্কেলের 9 mm এর দাগকে অতিক্রম করছে এবং 1 cm বা 10 mm এর আগেই শেষ হচ্ছে। তাহলে প্রধান স্কেল পাঠ হবে 9 mm (যে দাগকে পর্যন্ত অতিক্রম করছে)।
ভার্নিয়ার ধ্রুবক নির্ণয়
এখন 9 mm এর দাগের পর আরো কিছুটা গেছে। এই দূরত্বটুকু আমরা জানতে চাই। আমাদের ভার্নিয়ার স্কেলে দশটা দাগ কাটা। আমরা বলেছি ভার্নিয়ার স্কেলে ১০ দাগ থাকলে তা ৯ দাগের সমান হয়, মানে এই ১০ দাগ 9 mm এর সমান। ঐকিক নিয়ম অনুযায়ী প্রতিটি দাগ $\frac{9}{10}$ mm বা 0.9 mm। তাহলে প্রতিটি দাগ প্রধান স্কেলের ক্ষুদ্রতম দাগের থেকে 0.1 mm ছোট।
এটা অবশ্য ঐকিক নিয়মে করে আসা লাগবে না সবসময়। মূল স্কেলের ক্ষুদ্রতম প্রতি ভাগের দৈর্ঘ্যকে ভার্নিয়ার স্কেলের ভাগসংখ্যা দ্বারা ভাগ করে ভার্নিয়ার ধ্রুবক (VC) সরাসরি চলে আসবে।
VC = প্রধান স্কেলের ক্ষুদ্রতম এক ভাগের দৈর্ঘ্য / ভার্নিয়ার স্কেলের ভাগসংখ্যা
এক্ষেত্রে, VC = 1 mm / 10 = 0.1 mm
ভার্নিয়ার সমপাতন নির্ণয়
ছবিতে দেখা যাচ্ছে ভার্নিয়ার স্কেলের 6th দাগ প্রধান স্কেলের একটা ঘরের সাথে মিলে গেছে। তাহলে ভার্নিয়ার সমপাতন, V হলো 6।
ভার্নিয়ার স্কেল: কীভাবে কাজ করে?
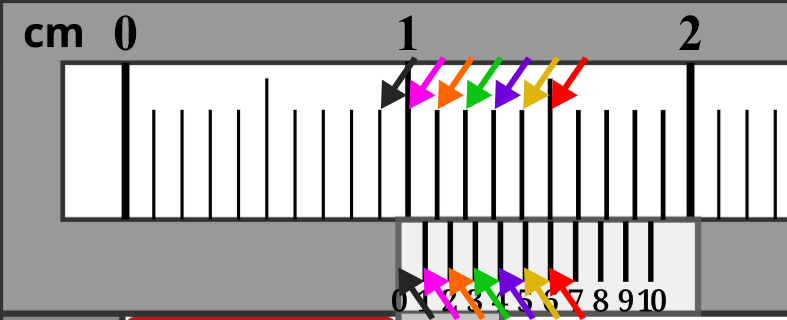
এখন আমরা একটু চিন্তা করি। ওপরের ছবিতে আমি স্কেলের অংশটুকু বড় করে দেখিয়েছি এবং কিছু তীর চিহ্ন যোগ করে দিয়েছি। দেখো, প্রধান স্কেলের লাল তীর দেয়া 6th দাগ আর ভার্নিয়ার স্কেলের লাল তীর দেয়া দাগ ঠিক একই বরাবর। মানে এদের মধ্যে দূরত্ব শূন্য।
কিন্তু হলুদ তীর দেয়া 5th দাগ আর প্রধান স্কেলের হলুদ তীর দেয়া দাগের একটু দূরত্ব আছে। এই দূরত্ব কত? আমরা যে ভার্নিয়ার ধ্রুবক নির্ণয় করেছি, সেটাই কিন্তু ছিলো ভার্নিয়ার স্কেলের এক ভাগ প্রধান স্কেলের এক ভাগ থেকে কতটুকু ছোট। তাহলে এই দূরত্ব হলো 0.1 mm।
একইভাবে প্রধান স্কেলের বেগুনি তীর থেকে ভার্নিয়ার স্কেলের বেগুনি তীর 0.1+0.1 mm বা 0.2 mm এগিয়ে। এরপর সবুজ দাগ 0.3 mm এগিয়ে, কমলা দাগ 0.4 mm, গোলাপি দাগ 0.5 mm এবং সবশেষে কালো দাগ 0.6 mm এগিয়ে।
আমরা যদি খেয়াল করি, আমাদের বস্তু কিন্তু প্রধান স্কেলের 9 mm এর দাগ থেকে এই দুই কালো দাগের যে দূরত্ব সেটুকুই এগিয়ে ছিলো। তাহলে আমরা আগের 9 mm এর সাথে 0.6 mm যোগ করে দিলেই বস্তুর টোটাল মাপ মেয়ে যাবো। মানে 9.6 mm।
ভালো কথা, এটা আমি অন্যরকম পাঠশালায় রাতুল ভাইয়ার ক্লাস থেকে শিখেছিলাম, সেই ভিডিওটা দেখে নিতে পারো।
ভার্নিয়ার স্কেলে পরিমাপ
আমরা আশা করছি ভার্নিয়ার স্কেল কীভাবে কাজ করে এটা বুঝতে পারছি। এখন আমরা সহজ একটা সূত্র দিয়ে এটা প্রকাশ করতে পারি।
দৈর্ঘ্য = M + V x VC
যেখানে M = প্রধান স্কেল পাঠ, V = ভার্নিয়ার সমপাতন, VC = ভার্নিয়ার ধ্রুবক
VC = প্রধান স্কেলের ক্ষুদ্রতম এক ভাগের দৈর্ঘ্য / ভার্নিয়ার স্কেলের ভাগসংখ্যা
আমাদের আগের হিসেবের বেলায় VC = 1 mm / 10 = 0.1 mm, M = 9 mm, V = 6
তাহলে, দৈর্ঘ্য = 9 mm + 6 x 0.1 mm = 9.6 mm
গাণিতিক সমস্যা: একটি বস্তুর দৈর্ঘ্য স্লাইড ক্যালিপার্সে মাপার সময় প্রধান স্কেলের পাঠ 1.4 cm, ভার্নিয়ার সমপাতন 7 পাওয়া গেলো। ভার্নিয়ার স্কেলের ভাগসংখ্যা 20। বস্তুর মাপ কত?
সমাধান:
এখানে প্রধান স্কেলের ক্ষুদ্রতম এক ভাগের দৈর্ঘ্য সরাসরি বলা হয়নি। আমাদের স্কেলে যেমন mm পর্যন্ত দাগ কাটা থাকে, এরকম প্রশ্নে বলা না থাকলে আমরা 1 mm ধরে নিতে পারি। অবশ্য প্রশ্ন থেকেও বোঝা যায়, 1.4 cm মানে 1 cm+4 mm, কাজেই mm এর ঘর পর্যন্ত আমরা প্রধান স্কেলে মাপতে পারছি।
এখন আমরা জাস্ট ভার্নিয়ার ধ্রুবক বের করে সূত্রে বসিয়ে দিব।
ভার্নিয়ার ধ্রুবক, VC = প্রধান স্কেলের ক্ষুদ্রতম এক ভাগের দৈর্ঘ্য / ভার্নিয়ার স্কেলের ভাগসংখ্যা = 1 mm / 20 = 0.05 mm
প্রধান স্কেল পাঠ, M = 1.4 cm = 14 mm
ভার্নিয়ার সমপাতন, V = 7
তাহলে, দৈর্ঘ্য = M + V × VC = 14 mm + 7 × 0.05 mm = 14 mm + 0.35 mm = 14.35 mm = 1.435 cm
[নোট: সবগুলো রাশি একই এককে না আনলে যোগ বিয়োগ করা যাবে না, যেকারণে প্রধান স্কেল পাঠকে mm এ রূপান্তর করে নেয়া। আমরা প্রধান স্কেল পাঠকে cm এ রেখে ভার্নিয়ার ধ্রুবককে cm এ রূপান্তর করতে পারতাম, তাতেও সমস্যা ছিলো না।
কোন সমীকরণ লেখার সময় ওপরের মত প্রতিটা রাশি এককসহ লেখা ভালো। এতে কোথাও এককের রূপান্তর প্রয়োজন কিনা, কোন এককগুলো গুণ বা ভাগ হচ্ছে সব স্পষ্ট থাকে। তবে এতে বাড়তি সময় প্রয়োজন, এবং কনসেপ্ট ক্লিয়ার হওয়ার আগে লদ্ধ একক নিয়ে কনফিউশন তৈরি হয়। যেকারণে পরীক্ষার খাতায় আমরা সাধারণত মাঝের লাইনগুলোতে একক লিখি না। অর্থাৎ এভাবে লিখি,
দৈর্ঘ্য = M + V × VC = 14 + 7 × 0.05 = 14 + 0.35 = 14.35 mm = 1.435 cm
উত্তর আমরা এখানে mm এককেও রাখতে পারতাম, এতে নাম্বার কাটা যেত না।]